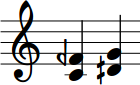
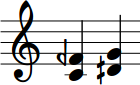
The semi-diminished fourth consisting of 12 steps in 31-ET is a strange interval, problematic from a theoretical perspective as it does not closely match any of the natural intervals in the harmonic series involving small harmonics. It comes somewhat close to the 13:10 ratio, but none of the other ratios involving small harmonics in the range of intervals matched well in 31-ET. It is one of the most xenharmonic intervals in 31-ET.
One of the closest matches of a just interval to this interval is (21:16), which can be called the septimal fourth. The septimal fourth can be represented as the difference between a septimal minor seventh (7:4) and a perfect fourth (4:3). If this sounds a bit esoteric and confusing to you, your impression is probably accurate: this is not an easily understood or easily heard interval.
This interval is very close to a perfect fourth, and it is often perceived as a flat fourth rather than any sort of third. It is for this reason that we shy away from the other possible name, the augmented third. This interval has an ambiguous and slightly atonal sound to it, but it is only mildly dissonant. In 12-ET, the tritone is the only wider interval that is harmonically ambiguous, but that interval is a strong, dominating interval. This interval, by contrast, is weak, and tends to blend into the background of a chord, imparting only a slight strangeness or tension, but allowing the other intervals to define the overall character.
The semi-diminished fourth, being so strange, is for the most part harmonically ambiguous. It matches certain just intervals in the harmonic series, but only ones that contain harmonics (such as 13 or 21) that are not well-incorporated into the 31-ET system. In theory, the Semi-diminished fourth, corresponding closely to the 21:16 septimal fourth, could imply the bottom note as root. If functioning as the 13:10 ratio (to which it is a poorer match), it would imply a root a whole tone beneath its lower note. In practice, however, because 31-ET does not handle or imply these sorts of harmonic relationships through any of the other intervals, it would be unlikely that this interval would imply either of these roots unless there was a strong harmonic context pointing to one of these notes as root.